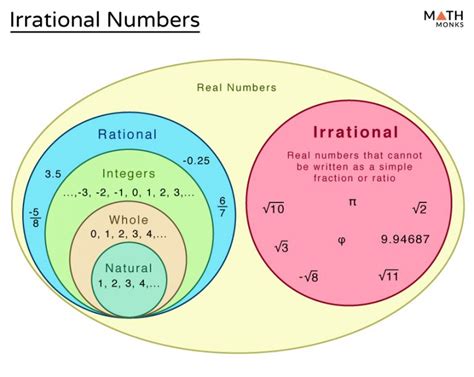
Mathematics has long been a field of both exactitude and wonder. Among its many discoveries, the realization that not all numbers can be expressed as a ratio of two integers stands out. This revelation, which emerged from the study of a seemingly simple geometric figure, the right triangle, fundamentally changed our understanding of numbers. One of the earliest and most significant discoveries in this realm was the square root of 2, an irrational number that continues to perplex and inspire mathematicians to this day.
Before delving into the implications of irrational numbers, it’s essential to understand the historical context. Ancient mathematicians, particularly the Greeks, held the belief that the universe could be described entirely through whole numbers and their ratios, known as rational numbers. This worldview was upended by the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The theorem itself was not groundbreaking—empirical knowledge of the relationship between side lengths of right triangles existed long before Pythagoras formalized it.
The truly earth-shaking discovery was the realization that for certain right triangles, the hypotenuse could not be expressed as a rational number. For instance, consider a right triangle with each of the other sides of length 1. The length of the hypotenuse in this case is the square root of 2 (√2). Through proofs not involving decimal approximations, it was demonstrated that √2 cannot be written as the ratio of two integers, making it an irrational number.
This was more than a mathematical curiosity; it was a profound philosophical and scientific upheaval. The acceptance of irrational numbers meant acknowledging that there are quantities that cannot be precisely measured using the existing number system of the time. It also posed a stark contrast to the previously unchallenged belief that all numbers were rational. Imagine living in an era where all known quantities could be neatly expressed through simple fractions, only to encounter a number that defies this neatly ordered system. It threw into question the completeness of the mathematical framework that the Greeks had built.
One of the intriguing facets of this discovery was how mathematicians dealt with it. There are legends, although historically debated, that the Pythagoreans tried to keep the existence of irrational numbers a secret because it was so contrary to their belief system. The revelation of √2’s irrational nature was akin to a heresy. However, over time, this groundbreaking concept was absorbed, and mathematicians began developing more robust systems to incorporate these ‘new’ numbers.
The discovery of irrational numbers was foundational for the field of mathematics as we know it today. It paved the way for the development of real numbers—those that include both rational and irrational numbers. This transition from a mathematical system based solely on rationality to one that accepts irrationality was monumental. Over centuries, mathematicians would continue to explore the properties of these irrational numbers, leading to further groundbreaking concepts such as the development of calculus and the formalization of the real number line.
Modern mathematics owes much to the ancient Greeks and the realization that not every number is rational. This journey from the empirical observations of right triangles to the abstract proofs of irrationality exemplifies the evolving nature of mathematical thought. As we continue to explore the depths of mathematics, the story of √2 remains a testament to the field’s ability to challenge and expand our understanding of the universe. The journey from rational to irrational numbers, and the subsequent mathematical developments, highlight not just the progress in mathematics but also how deeply intertwined it is with our quest to understand the world in all its complexity.

Leave a Reply